In 1936, Alan Turing, the father of computer science, proposed a hypothetical machine which is capable of implementing any computer algorithm that exists (Clark and Steadman, 2017). Despite the fact that it is a hypothetical machine in its core, it was the first proposed machine which store functions in its memory rather than modifying its physical structure to use new functions (Clark and Steadman, 2017). We can see that along with the famous mathematician and his supervisor Alonzo Church, Turing’s work involving Turing machines allowed the way for modern computer systems and programming languages to observe the problem solving capabilities and limitations in modern computation. This article will explore the concepts and theories of Alan Turing and their relation to modern computer science.

First, let’s look at what a Turing machine is. Even though it is a hypothetical machine, its hypothesis is based on a physical machine. The machine consists of a tape that is infinitely long and that is divided into squares, which acts like a memory in this context, and a head which is positioned over one of the squares which includes symbols in it (Mullins, 2012). The machine can perform operations based on the head and the state determined by the symbol on the head square such as reading and editing it. With these operations, we can create as many states as we want to compute complex functions, which leads to this machine being able to run any computable algorithm in it.
So how do we define the computability of algorithms that can be run in a Turing machine? This is a question that is tried to be answered by the Church-Turing thesis. The common interpretation of this thesis states that any kind of “effective” computation can be done by a Turing machine. However, the “effective” part here is important because since we cannot formally define what an effective computation is, we therefore cannot prove the Church-Turing thesis either even though it is universally accepted in the computer science domain. Furthermore, we also need to know every computation that exists in order to show that every computation can be done using a set of techniques which is the main claim of the Church-Turing thesis in first place. Tychonievich (2011) explains the thesis really well in simple words: “if it can be done, it can be done by a computer”. If we can solve a problem in reality, we can solve it using Turing machines too.
It is very important to dive more into the characteristics of the hypothetical Turing machine in order to see its relations to modern computer systems and programming languages. Turing machines work with important assumptions: it has an infinite amount of memory and it will compute any algorithm no matter how much time it takes to compute it (De Mol, 2018). Based on these assumptions, we can observe that modern computer systems are more of finite examples of Turing machines since they don’t have infinite amount of memory, which makes some existing computable algorithms that need more memory than the system already has in it unable to be computed by these systems.
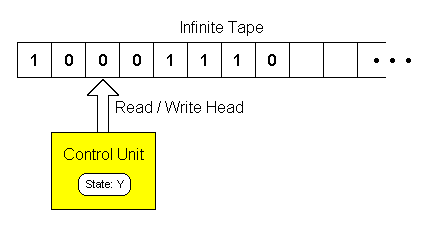
Based on the provided descriptions above, we can conclude that given enough memory and time, any machine that can solve any computational problem in any complexity is a Turing complete machine. This conclusion is valid for a Turing machine, and therefore if we can compute an algorithm on a modern computer system like desktops and laptops, and that we can compute that algorithm on a Turing machine as well, we can say that modern computer systems can be described as Turing complete systems.
This may lead to the question of the existence of a non Turing complete system today. Well, if a machine cannot solve any computational problem given enough memory and time like home computers, we can say that this machine is not Turing complete. For example, a simple calculator can do only 4 operations: addition, subtraction, multiplication and division. But that’s it. You cannot do any more operations on a calculator. This limitation makes a simple calculator a Turing incomplete machine.
What about programming languages? Well, the vast majority of the programming languages such as C++, Python and Java that are used in various applications are Turing complete because they can work with the characteristics and assumptions of a Turing machine: they have looping functions such as for loops and while loops that can allow a program to run as long as we want (even for an infinite amount of time) and they can access and edit memory with functions for reading, writing and memory allocation. If a programming language does not have functions that do not allow the language to work with these characteristics and assumptions, then we cannot simulate a Turing machine and therefore the language would be Turing incomplete. An example for a Turing incomplete programming language is Charity, which is a functional programming language that is restricted to be used for functions that will be terminated at one point, therefore not allowing the function to run for an infinite amount of time (The Charity Development Group, 1996).
In addition, I would also like to talk a bit about a problem with Turing machines: the halting problem. The halting problem asks for a generalised algorithm that can determine whether a program will terminate or not given an arbitrary program and input. Alan Turing proved in 1936 that no generalised algorithm can exist to solve the halting problem, therefore making it undecidable, since we cannot know if the program will halt with that input before running the program (Moore et al., no date). If you tried to find the solution by running the program, you would never know what would exactly happen since the program could potentially run forever, or would take such a massive amount of time that would seem infinite to you when it technically is not. You might say that a program would eventually halt on a physical perspective due to running out of electricity or by closing the machine, but considering a Turing machine which is pretty much a mathematical concept, you would ignore physical limitations on this problem. The halting problem shows that there are problems that cannot be solved even by computers.
In conclusion, the mathematical concepts of a Turing machine and Turing computability served as foundational models for modern computation with contemporary computers and programming languages. Computers are now an essential part of our lives and we use them to solve many complex problems that we cannot easily solve by ourselves, but in the end, there will be problems that we can describe, but unable to solve even with computers, and even with a Turing machine if we could exactly build one.
References:
Clark, L. and Steadman, I. (2017) Remembering Alan Turing: From codebreaking to AI, Turing made the world what it is today, WIRED UK. Available at: https://www.wired.co.uk/article/turing-contributions (Accessed: October 25, 2022).
De Mol, L. (2018) Turing machines, Stanford Encyclopedia of Philosophy. Stanford University. Available at: https://plato.stanford.edu/entries/turing-machine/ (Accessed: October 25, 2022).
Moore, K. et al. (no date) Halting Problem, Brilliant Math & Science Wiki. Available at: https://brilliant.org/wiki/halting-problem/ (Accessed: October 26, 2022).
Mullins, R. (2012) What is a Turing machine?, Department of Computer Science and Technology – Raspberry Pi: Introduction: What is a Turing machine? Available at: https://www.cl.cam.ac.uk/projects/raspberrypi/tutorials/turing-machine/one.html (Accessed: October 26, 2022).
The CHARITY Home Page (1996) Charity. The Charity Development Group. Available at: http://pll.cpsc.ucalgary.ca/charity1/www/home.html (Accessed: October 26, 2022).
Tychonievich, L. (2011) The Church-Turing Thesis, The church-turing thesis. Available at: https://www.cs.virginia.edu/luther/blog/posts/116.html (Accessed: October 25, 2022).
